LSTM Equations Explained: Derivation & Math Tutorial

---

Introduction to LSTM Equations

Understanding lstm equations is crucial for anyone diving deep into recurrent neural network theory. This guide explains the math underpinning LSTM: gate activations, forward pass, backward pass gradients, and chain‑rule derivations. Whether you’re implementing from scratch or debugging training, this lstm equations tutorial equips you with clarity and precision.

---

1. LSTM Gate Equations and Forward Pass

At each time step t, an LSTM cell computes:

Then the cell and hidden states update:

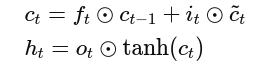
This lstm equations explained section clarifies how inputs and previous states combine to compute new internal states.

---

2. Backward Pass: Gradient Derivations

To train with backpropagation through time, we compute partial derivatives:

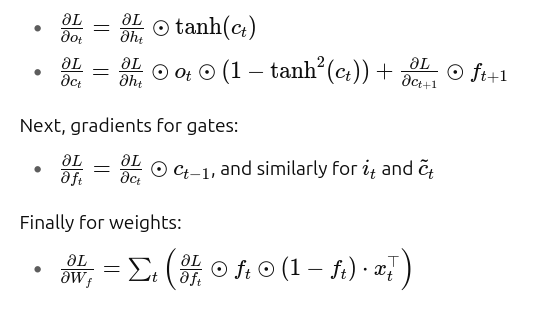
This section shows full lstm equations backward pass derivations with chain‑rule and matrix calculus.

---

3. Gate Activation and Nonlinearity Jacobians

Gate activations use sigmoid or tanh:

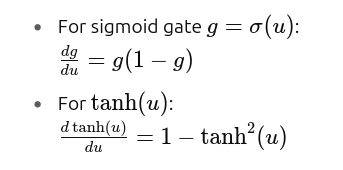
4. Gradient Flow and Vanishing/Exploding Stability Conditions

The derivative of

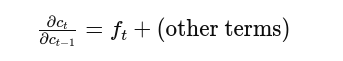
If forget gate output ftf_tft​ is close to 1, gradients flow well; if too small, vanishing occurs. Proper initialization and clipping prevent blow-ups. This is part of lstm equations gradients analysis.

---

5. Step-by-Step Numerical Example

Consider a toy example:

• Input xtx_txt​ is scalar
• Choose small weight and bias values

6. Implementation Tips & Debugging Based on Equations

• Use consistent weight initialization (e.g., Xavier/Glorot)
• Monitor gate activations: if any gate saturates (0 or 1), gradient flow may vanish
• Clip gradients: based on ∂L/∂ct​ magnitude
• Validate manually computed gradients using finite differences

Implementing LSTM from scratch helps cement the theory behind lstm equations implementation and supports debugging deep learning frameworks.

Links & Further Mathematical References

• Matrix calculus reference: Deep Learning Book appendix
• Recurrent neural nets and BPTT: Christopher Olah blog
• Comprehensive LSTM derivation: arXiv tutorial papers

---

✅ Frequently Asked Questions (FAQs)

1. Why are gate activations necessary in LSTM?
   Gates regulate the flow of information and control memory updates, preventing vanishing gradients.
2. How do we derive the backward pass for LSTMs?
   Using chain rule via partial differentiation through time for each gate and cell state update.
3. What causes exploding gradients in backward pass?
   Large values of ftf_tft​ repeated over many steps can amplify gradients unless clipped.
4. Should I implement these equations myself?
   Yes—it deepens understanding and aids debugging, even if frameworks automate it.
5. Where can I find a code implementation based on these derivations?
   Popular educational resources and GitHub repositories often reproduce full lstm equations from scratch implementations with unit tests.

🧩 Get Started: Check Out These Guides on Python Installation

Working with LSTM neural networks often means setting up Python correctly, managing multiple versions, and creating isolated environments for your deep learning experiments.

To make sure your LSTM models run smoothly, check out these helpful blogs on Python installation:

📌 Python 3.10 Installation on windows

📌 Python 3.13 (latest) installation guide – easy and quick installation steps